
One may choose to use one test over the other depending on context, but a t ratio is typically used for regression tests.įor more information about the linear regression, we can click the red triangle next to “Linear Fit” under the graph. In simple linear regression, these two values will match because they are testing the same thing. They two tests are different in that the parameter estimates uses a t test to form a t ratio, and the ANOVA partions the SStotal into SSregression and SSerror.
This p-value is exactly the same as the one calculated in ANOVA. Show your forecast below and attach the completed Excel template. Call Volume Forecast for July 2015 (Causal Forecasting based on head count): Question: Apply Linear Regression to predict call volume from head count using the appropriate Excel template. We are given the estimate of the slope of 1.77, the estimated standard error of 0.15, a t ratio of 11.77 formed by dividing the estimated slop by dividing the slope by the standard error, and a p-value of 0.0003 calculated from the t distribution. Show your forecast below and attach the completed Excel template. The standard error for intercept is substantially smaller because the formula for intercept has many more terms which could have the potential for more things to go wrong. we are also given the hours (slope) that is adding 1.77 hours for the grade that is expected. We are given the intercept estimate of where the line hits the y axis and we are given our t ratio and a p-value that is received from our appropriate t distribution. (Actual sample estimate - Expected H 0)/ (Standard Error) Linear regression is a statistical method for determining the slope and intercept parameters for the equation of a line that best fits a set of data. 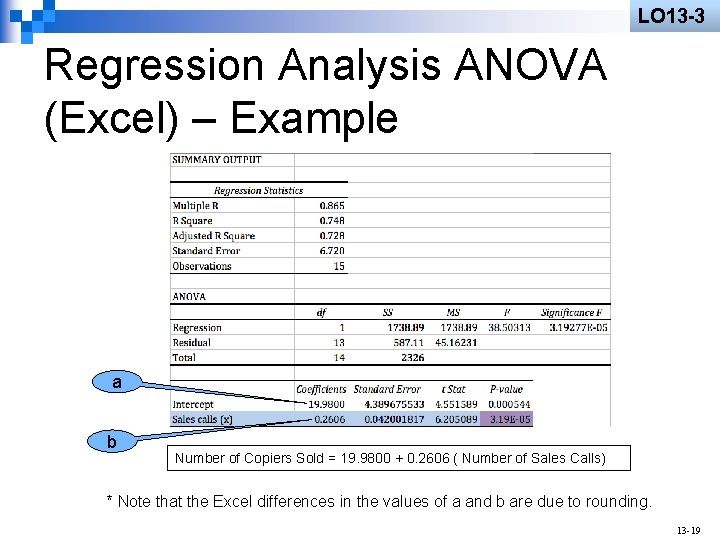
The Parameter Estimates output gives these statistics in the form of t statistics.





 0 kommentar(er)
0 kommentar(er)
